Algebra

JamworksPro Takes Online Graphing Seriously

by jaye

Jaye at JamworksPro has been busy over the past few months polishing his Flagship Multivariate Algebraic Expression Based Graphing Calculator, Math Dynamics. It’s more than just a graphing calculator. It’s an entire Mathematics Management System.

Warrenton Oregon, Oct 28, 2021— From the JamworksPro R&D Department Comes Math Dynamics, the Online Arithmetic Machine (https://mathdynamics.net). Math Dynamics includes both an Android App as well as it’s Complementary Web App. At the core of Math Dynamics is the ability to write mathematical expressions using most nearly any string of alphanumeric characters as variables.

“Math doesnt have to be cryptic”

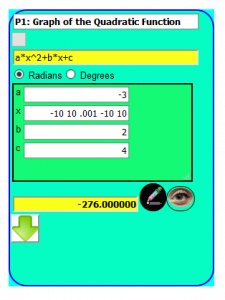
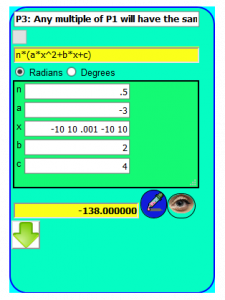
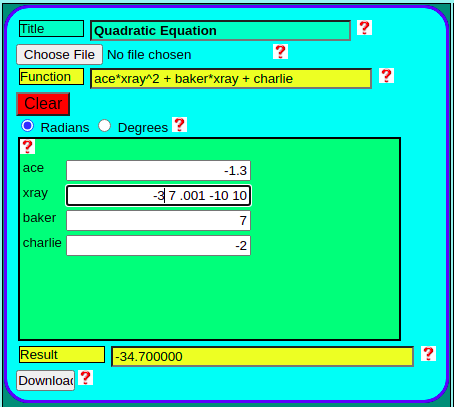
a*x^2 + b*x + c
can also be written as
ace*xray^2 + baker*xray + charlie

Math Dynamics keeps it simple with a straight forward approach to variables, constants and the operators used to form mathematical expressions.

If  h is the height measured in feet,  t  is the number of seconds the object has fallen from an initial height h0 with an initial velocity or speed v0 (ft/sec), then the model for height of a falling object is: 

h(t)=−16 * t^2 + v0 * t + h0

“Free Form Variable Names make more sense in the physical world”

height(elapsedTime) = -16 * elapsedTime^2 + initialVelocity * elapsedTime + initialHeight

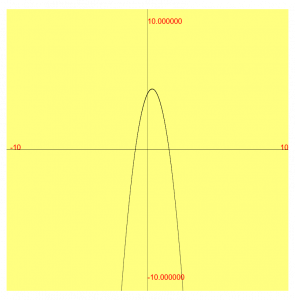
Mathematical Expressions are packaged in Math Dynamics as Function Definition Cards. The Variables are listed in a table that allows their values to be edited. Any one of the variables can be used as an independent variable to plot the graph of the function. By entering start, end and increment values in that order will define that variable as independent and will plot a graph accordingly. Function Definition Cards can be named and saved as .xg2 files for portablility. These .xg2 files can be opened by both the Web App as well as the Android App.

This Function Definition Card demonstrates the straight forward approach to assigning meaningful names to the variables.
This Function Definition Card defines the Quadratic Function in terms that have coefficients with free form names. Note that the value of the ‘xray’ term defines the x axis limits as -3 to 7, an increment of .001 and y axis limits as -10 to 10.

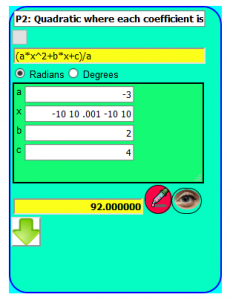
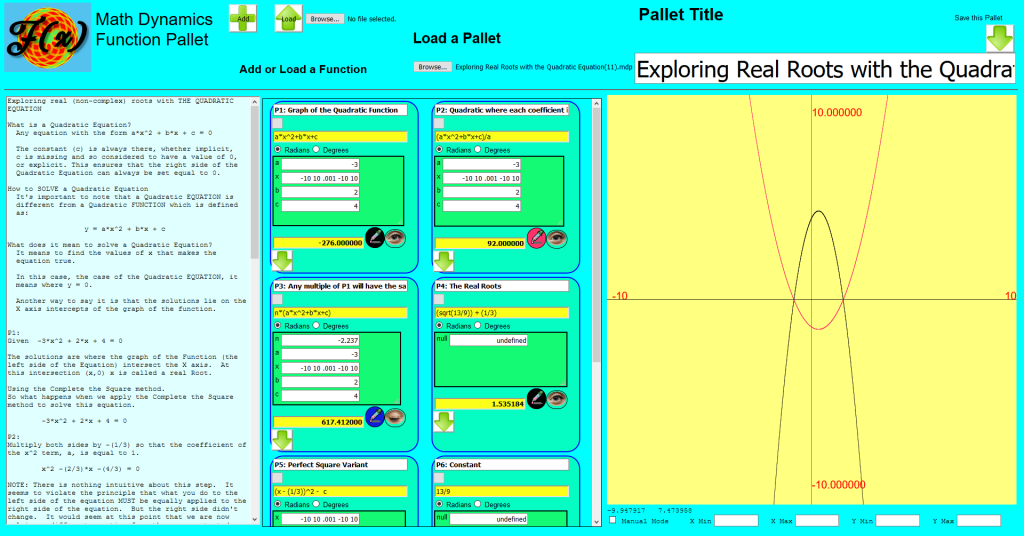
Collections of Function Cards are packaged in the Math Dynamics Pallet (https://mathdynamics.net/pallet.html). Both the Android App and the Web App have a Pallet. Function Definition Cards are easily added to or removed from the Pallet. The Pallet in the Android App supports Function Definition Cards that each have a self contained graph while the Pallet in the Web App supports a single graph on which any of the Function Definition Cards may use to plot its graph.

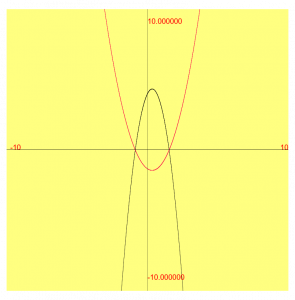
The Pallet in the Web App is very powerful. It supports plotting multiple functions on the same graph. Each plot can have a different color and each plot can also be hidden. Like Function Definition Cards, Pallets can be named and can be downloaded and saved for portability.

The Web App Pallet supports up to 26 custom functions. Each function can be plotted on the common graph. The visibility of the graph can be turned on or off. Each graph can have a custom color assigned to it.
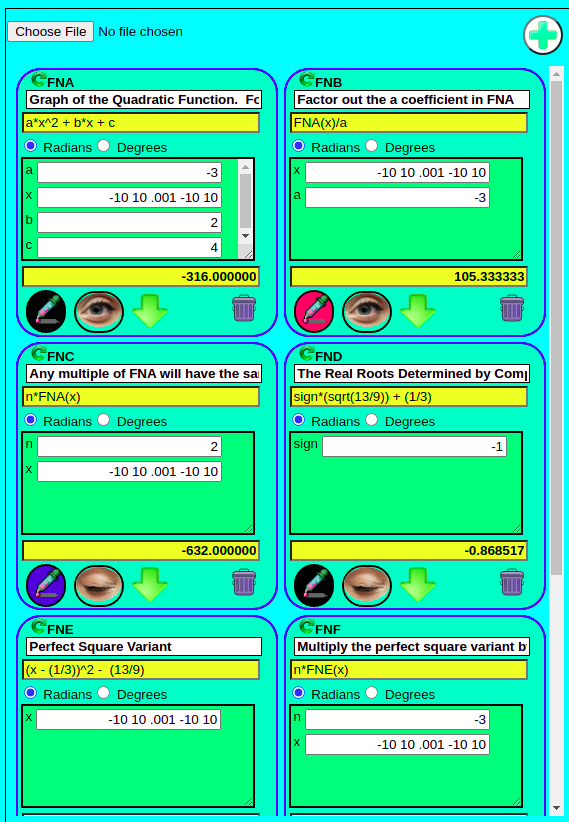
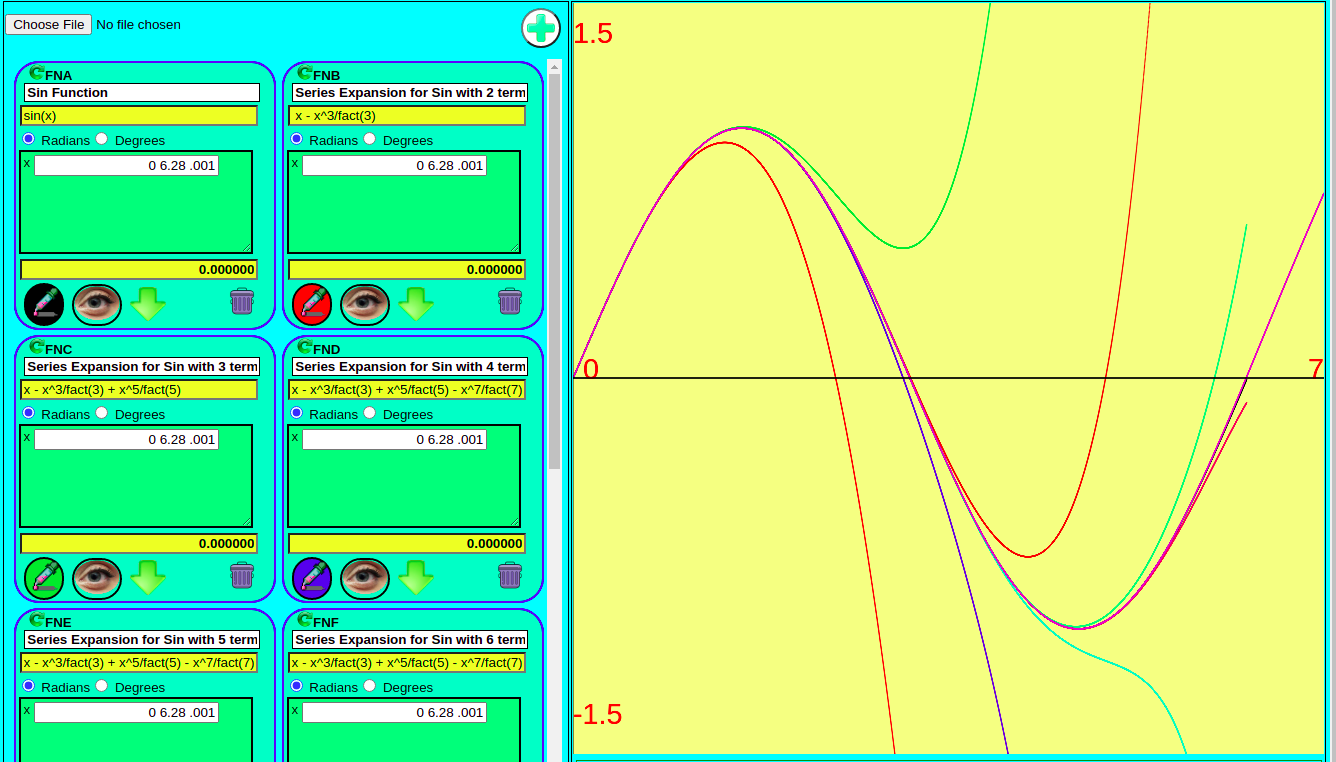
The Math Dynamics Function Pallet provides a way to graph multiple functions on the same graph
This Graph of the Maclaurin Series to calculate the sin of an angle demonstrates the ability to plot multiple functions on the same graph.

Each Function Definition Card in the Math Dynamics Web App Function Pallet is assigned its own three letter moniker. A Function moniker always begins with FN and the third letter is determined by the position of Function Definition Card in the Pallet. For example the first Function Definition Card will have the moniker FNA and the second, FNB. The Math Dynamics Web App Pallet supports 26 of these function monikers, FNA thru FNZ.

These monikers allow each Function Definition in the Pallet to used as an intrinsic function such as sin(), cos(), sqrt(), etc.. in any other Function Definition Card. The argument of the calling Function will be passed to the called Functions independent variable.

The Math Dynamics Web App Function Pallet is designed for training and research. The Web App contains an editor in the left panel that is used to write details and instructions about the Pallet, allowing entire tutorials to be created. Using the Pallet Download and Load features provides for great portability.

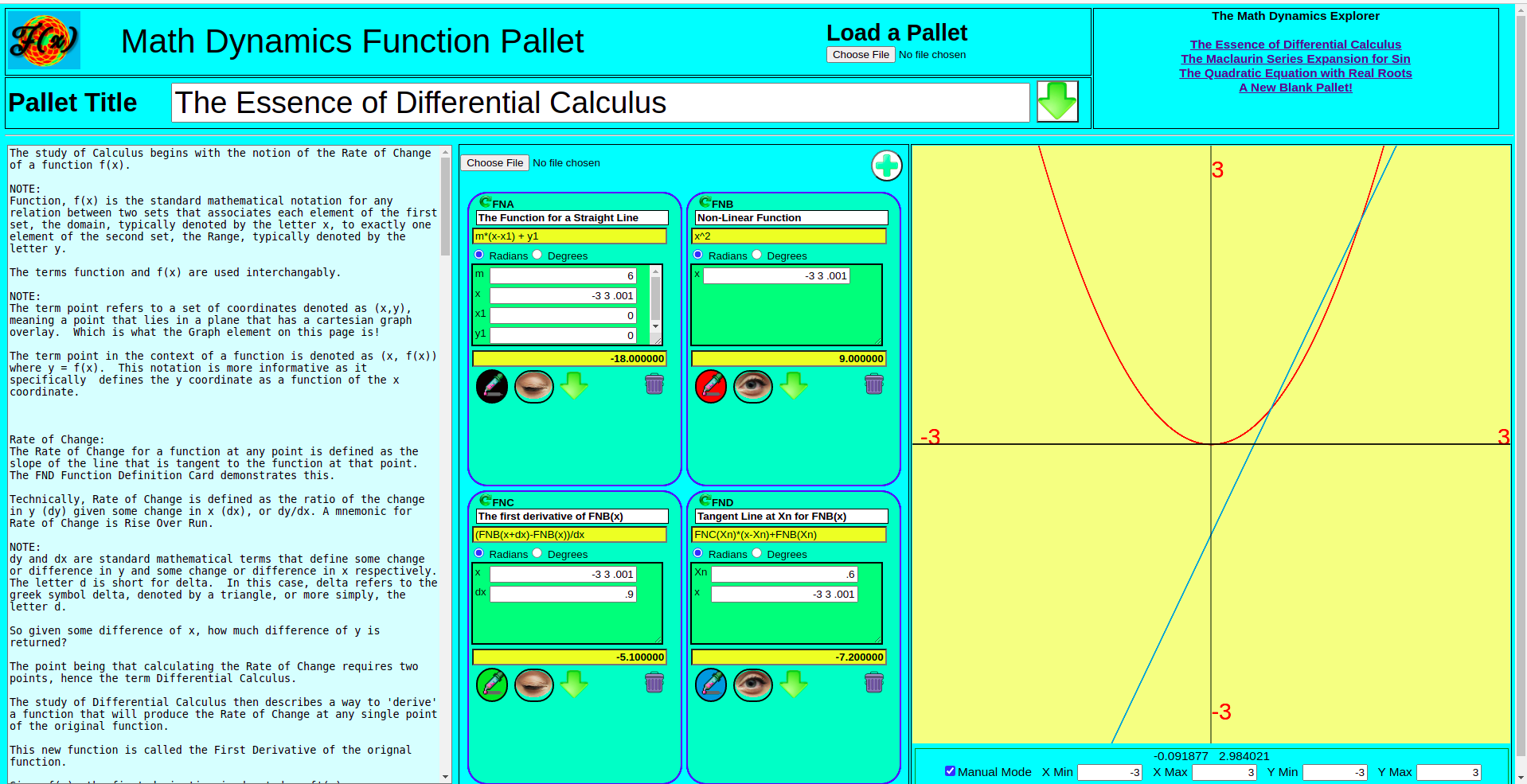
This Math Dynamics Function Pallet provides a tutorial on the fundamental concepts of Differential Calculus.

Jaye Mosier, owner of JamworksPro is an Independent Software Developer specializing in small business web development as well as android mobile app development. Complex back end data systems interfaced with simple and elegant GUI design is one of Jaye’s many specialties.

Jaye (https://jaye.jamworkspro.com) has published many software title over the years including FileNotes, TRAX, Coupon Cache and others as well as the most recent projects, Math Dynamics, Vibrology App and The Pothole Project.

A Quadratic Deep Dive into Real Roots

by jaye

The Math Dynamics Multivariable Algebra Expression Based Graphing Calculator

Graph of the Quadratic Equation
This Math Dynamics Function Card will generate a plot from -10 to 10 in increments of .001 and limit the Y axis from 10 to -10

Complete the Square method is an algorithm to find the Roots of a Quadratic Equation both Real and Complex.  This exercise focuses on using the “Complete the Square” method to calculate the Real Roots so it only makes sense to use a Quadratic Function that has two real roots.

We start with a Quadratic Function defined as:

\( -3*x^2 + 2*x + 4 \)

The plot of this function visually demonstrates that this Quadratic Function has 2 real roots. 

The exact values of these two real roots can be calculated using the “Complete the Square” method.  This requires two things:

  1. \( -3*x^2 + 2*x + 4 = 0\)
  2. The \(a*x^2\) term requires that a = 1, not -3
Quadratic where the coefficient of the x^2 term is always 1
This Math Dynamics Function Card produces a Quadratic Equation that factors out the coefficient a ensuring it is always 1

To resolve the second requirement requires that both sides of the quadratic equation be multiplied by -(1/3) such that the new Quadratic Function is:

\( x^2 -(2/3)*x -(4/3) = 0\)

Which produces a different graph.  This new graph shares the same roots as the original graph.

I found this to be a quite interesting property.  It appears though that all multiples of a Quadratic Function have equal roots

Visual evidence that all multiples of any quadratic function have the same roots
This Math Dynamics Card defines a function that can generate any multiple of any Quadratic Function
Math Dynamics Function Pallet exploring the Quadratic Equation
Explore the Quadratic Equation and Using the Complete the Square Method to find the roots.