algebra expression

A Quadratic Deep Dive into Real Roots

by jaye

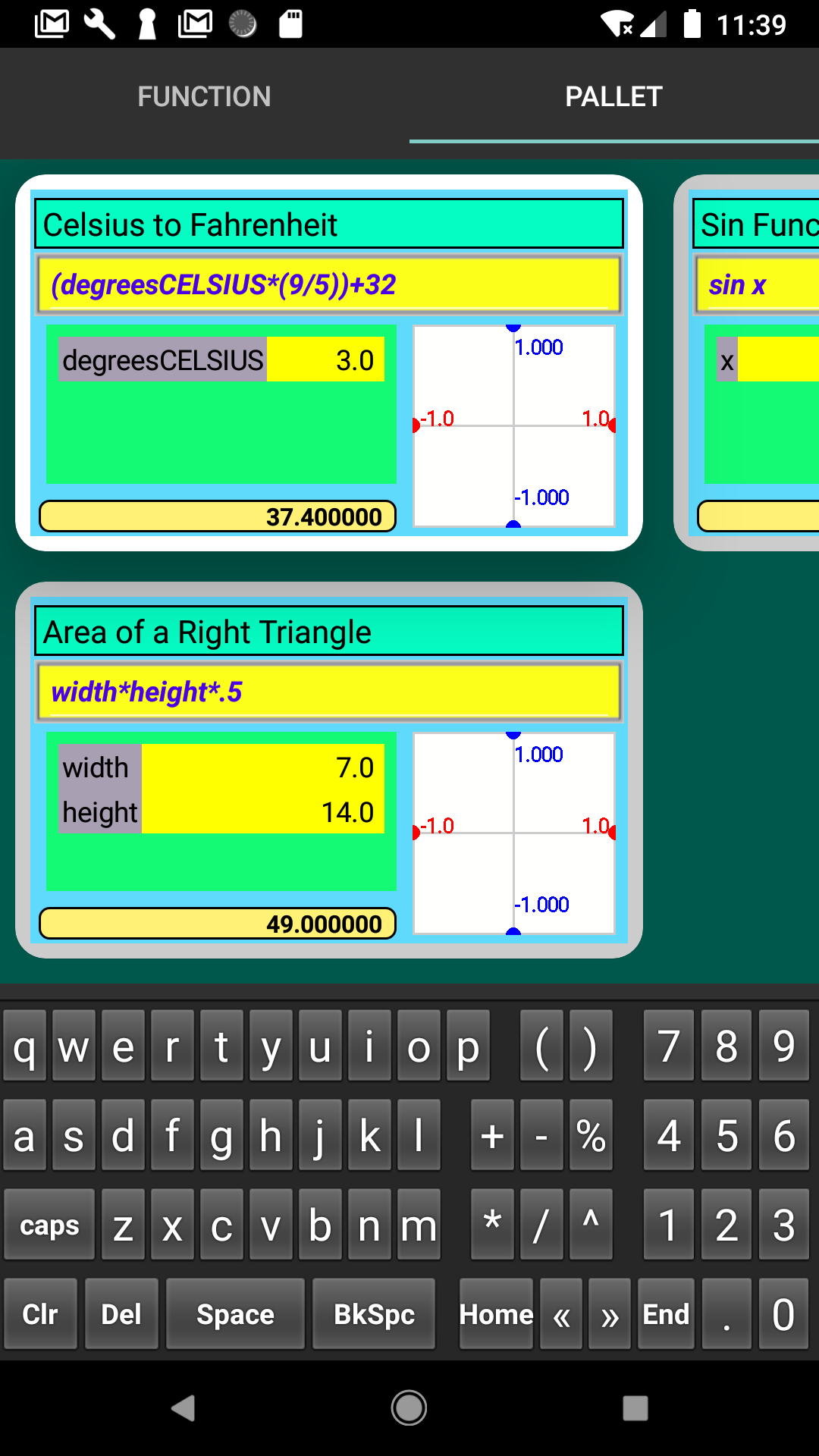
The Math Dynamics Multivariable Algebra Expression Based Graphing Calculator

Graph of the Quadratic Equation
This Math Dynamics Function Card will generate a plot from -10 to 10 in increments of .001 and limit the Y axis from 10 to -10

Complete the Square method is an algorithm to find the Roots of a Quadratic Equation both Real and Complex.  This exercise focuses on using the “Complete the Square” method to calculate the Real Roots so it only makes sense to use a Quadratic Function that has two real roots.

We start with a Quadratic Function defined as:

\( -3*x^2 + 2*x + 4 \)

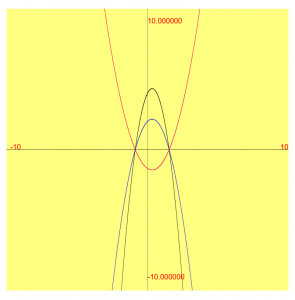
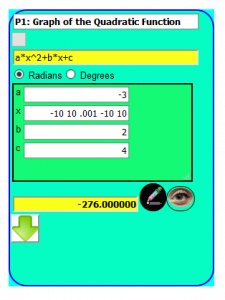
The plot of this function visually demonstrates that this Quadratic Function has 2 real roots. 

The exact values of these two real roots can be calculated using the “Complete the Square” method.  This requires two things:

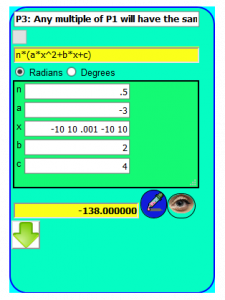
  1. \( -3*x^2 + 2*x + 4 = 0\)
  2. The \(a*x^2\) term requires that a = 1, not -3
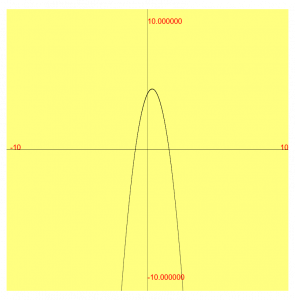
Quadratic where the coefficient of the x^2 term is always 1
This Math Dynamics Function Card produces a Quadratic Equation that factors out the coefficient a ensuring it is always 1

To resolve the second requirement requires that both sides of the quadratic equation be multiplied by -(1/3) such that the new Quadratic Function is:

\( x^2 -(2/3)*x -(4/3) = 0\)

Which produces a different graph.  This new graph shares the same roots as the original graph.

I found this to be a quite interesting property.  It appears though that all multiples of a Quadratic Function have equal roots

Visual evidence that all multiples of any quadratic function have the same roots
This Math Dynamics Card defines a function that can generate any multiple of any Quadratic Function
Math Dynamics Function Pallet exploring the Quadratic Equation
Explore the Quadratic Equation and Using the Complete the Square Method to find the roots.

JamworksPro Introduces Math Dynamics™ for Android

by jaye

Math Dynamics, the Multivariate Algebraic Expression Based Graphing Calculator

Math Dynamics is more than a calculator. It’s a platform for managing math intensive information. From simple unit conversions to advanced algebraic and trigonometric analysis. Math Dynamics allows the User to craft custom Function Definitions from many discipline’s such as Statistics, Marketing, Engineering, etc.

Its a tool for Math. Another instrument that you can add to your tool chest that gives you an edge when it comes to everyday activities that demand a quick calculation.

Use Calculator mode for a quick calculation. Calculations can range from simple arithmetic to multivariate formulas like Cost per Unit, Miles per Gallon, etc..

 

Any formula created in the Calculator can be saved to the Pallet.

The Pallet is a collection of Function Definition Cards. Each card contains the function definition and a list of all of the variables defined and it’s evaluated result. Users can quickly evaluate any Function Definition simply by editing the values of the variables in the table. The result is evaluated in real time as you change the values of the variables.

With Math Dynamics you can share your function definitions with other users. Export and Import functions allow the Users to save and share any of the Function Definition’s in the Pallet as a Math Dynamics XML file. These files also include the values of the variables, the result and the Trig Mode at the time of Export.