Trigonometry is based on the fundamental principle of ONE length.  The length in this context is immaterial because with Trigonometry we only need be concerned about ONE.  For example if you draw a circle it is ONE circle no matter how big or small.  Because it is a circle it has only ONE center with a constant distance to the edge of the circle.  This constant distance is ONE and is called the Radius.

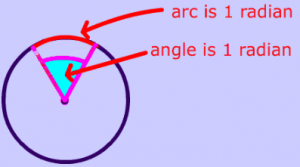
Simple so far, just a circle with a center and a radius of ONE.  Now consider the radius as it sweeps through a small region of the circle forming a triangle with two sides of an equal length ONE  and forming an angle at the apex of the triangle.  An Angle is a unit that specifies the amount of the sweep of the radius that formed the triangle.

At this point we are finished with the circle.  It is no longer needed.  Also, our Triangle can now be moved and reoriented any way we wish. 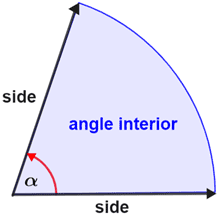 It is imperative though that the lengths of the two radii forming the triangle remain equal and ONE.  The angle is most visually apparent when one of the sides of the Triangle lies along a horizontal axis.  At this point a perpendicular line can be drawn between the tip of one of radii and intersecting the other radii.  The perpendicular line intersects the radii  such that the length between the apex (angle)  and the intersection is a ratio of ONE.

Now, this is where it gets complicated.  Since the triangle has been conveniently aligned with one of the radii along the horizontal axis it can be said that the SIN is the distance (as a percentage of ONE) along a corresponding VERTICAL AXIS between the TIP of one radii and a HORIZONTAL AXIS.  Likewise the COS is the distance along a HORIZONTAL AXIS  between the TIP of one radii and a VERTICAL AXIS.

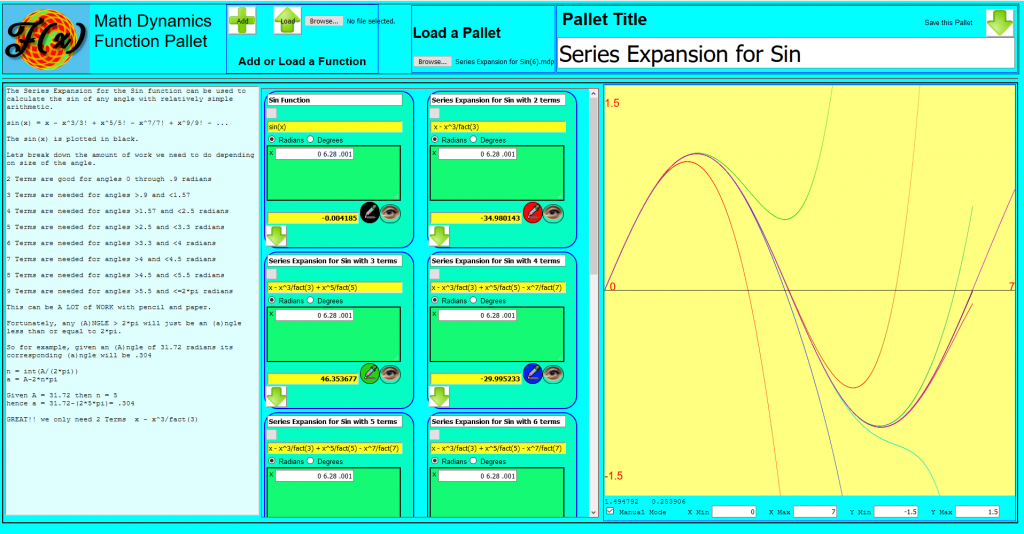
Explore things like; How many terms do I need to get an accurate calculation for any angle.   Find out with the  Math Dynamics Multivariate Algebraic Expression Based Graphing Calculator.

Click here for the live interactive Pallet